Bósónì

Ninu fisiksi eleruku, awon bosoni ( /ˈboʊsɒn/) je eruku inuatomu pelu nomba odidi spin (s = 0, 1, 2 etc.) ti won tele ilana statistiki Bose-Einstein. Oruko bosoni wa latowo Paul Dirac lati se eye fun ipa ti asefisksi ara India Satyendra Nath Bose, pelu Albert Einstein, ko ninu idasile statistiki Bose-Einstein—arojinle to unselana ninu eyi. Ninu awon Bosoni ni bosoni Higgs (s=0), awon mesoni (s=0,1), grafitoni aladalaba (s=2), iyewu adurosinsin nomba akojo didogba (f.a., deuterium, helium-4, lead-208) ati awon aruku to pondandan lati se papa arojinle papa oniyebintin bi awon fotoni, awon gluoni, at.b.b.lo. Awon bosoni yato gidigidi si awon eka eruku inu atomu ti a mo si fermioni nibi pe ko si opin si iye to le wa ni aye oniyebintin kanna. Iwa yi, fun apere, lo unfa ini pataki helium-4 nigba to ba je titutu de superfluid.

Afijuwe Olopagun awon eruku alapilese, pelu awon bosoni afiwon ni orila-anaro to gbeyin

Awon ini bosoni

Bosons contrast with fermions, which obey Fermi–Dirac statistics. Two or more fermions cannot occupy the same quantum state (see Pauli exclusion principle).

Since bosons with the same energy can occupy the same place in space, bosons are often force carrier particles. In contrast, fermions are usually associated with matter (although in quantum physics the distinction between the two concepts is not clear cut).

Bosons may be either elementary, like photons, or composite, like mesons.

All observed bosons have integer spin, as opposed to fermions, which have half-integer spin. This is in accordance with the spin-statistics theorem, which states that in any reasonable relativistic quantum field theory, particles with integer spin are bosons, while particles with half-integer spin are fermions.

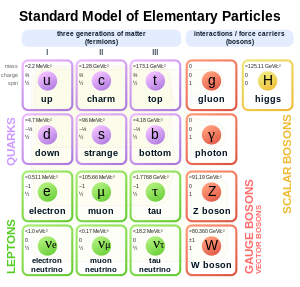
While most bosons are composite particles, in the Standard Model, there are five bosons which are elementary:

• the four gauge bosons (Error no link defined · g · Error no link defined · Error no link defined)
• the Higgs boson (Error no link defined)

Additionally, the graviton (G), a hypothetical elementary particle not incorporated in the Standard Model, if it exists, must be a boson, and could conceivably be a gauge boson.

Composite bosons are important in superfluidity and other applications of Bose–Einstein condensates.

Itumo ati ini pataki

By definition, bosons are particles which obey Bose–Einstein statistics: when one swaps two bosons, the wavefunction of the system is unchanged. Fermions, on the other hand, obey Fermi–Dirac statistics and the Pauli exclusion principle: two fermions cannot occupy the same quantum state, resulting in a "rigidity" or "stiffness" of matter which includes fermions. Thus fermions are sometimes said to be the constituents of matter, while bosons are said to be the particles that transmit interactions (force carriers), or the constituents of radiation. The quantum fields of bosons are bosonic fields, obeying canonical commutation relations.

The properties of lasers and masers, superfluid helium-4 and Bose–Einstein condensates are all consequences of statistics of bosons. Another result is that the spectrum of a photon gas in thermal equilibrium is a Planck spectrum, one example of which is black-body radiation; another is the thermal radiation of the opaque early Universe seen today as microwave background radiation. Interactions between elementary particles are called fundamental interactions. The fundamental interactions of virtual bosons with real particles result in all forces we know.

All known elementary and composite particles are bosons or fermions, depending on their spin: particles with half-integer spin are fermions; particles with integer spin are bosons. In the framework of nonrelativistic quantum mechanics, this is a purely empirical observation. However, in relativistic quantum field theory, the spin-statistics theorem shows that half-integer spin particles cannot be bosons and integer spin particles cannot be fermions.

In large systems, the difference between bosonic and fermionic statistics is only apparent at large densities—when their wave functions overlap. At low densities, both types of statistics are well approximated by Maxwell-Boltzmann statistics, which is described by classical mechanics.

Elementary bosons

Ẹ tún wo: List of particles#Bosons